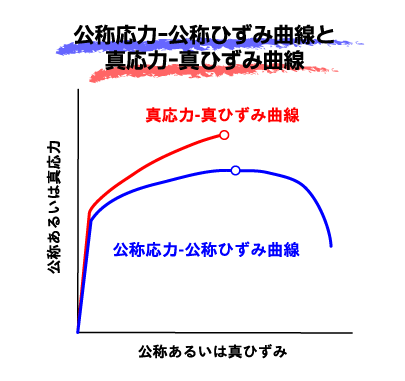
引張試験から得られた荷重-伸び曲線から，応力-ひずみ曲線を求めることができます． 同じ材料でも，試験片の形状によって平行部断面にかかる荷重やひずみ量は異なります．荷重(P)を初期断面積(S₀)で割ったものを公称応力(Nominal stress: s)，伸び(Dl)を初期平行部長さ(L₀)で割ったものを公称ひずみ(Nominal strain: e)と言います．

s=P/S₀, e=Dl/L₀

一方で，変形の進行とともに平行部断面積や平行部長さは変化します．正確な応力とひずみの関係を知るためには，時々刻々と変化するこれらの値を考慮する必要があります．このときの応力とひずみを，それぞれ真応力(True stress: s)，真ひずみ(True strain e)と言います．真応力(s)と真ひずみ(e)は，公称応力(s)と公称ひずみ(e)を用いて次の式で定義されます．

上の2式は試験片平行部が均一変形している領域において成り立ちます．応力と加工硬化率の関係が塑性不安定条件^*を満たし，試験片がくびれるような変形(局所変形と言います)においては成立しません．ですので，真応力-真ひずみ曲線は荷重-伸び曲線における最高荷重点(引張強さ)までとなります．